
La matematica più pura
- Miriadi di granelli di sabbia e di chicchi di frumento
- Storia della fine del mondo
- Una stampante “universale”
- Come contare l’infinito
- La matematica più pura
- La misteriosa radice di meno uno
- Proprietà inconsuete dello spazio
- Geometria senza misure
- Rovesciare lo spazio
- Il tempo è la quarta dimensione
La matematica di solito è considerata, specialmente dai matematici, la Regina di Tutte le Scienze ed essendo una regina, cerca di evitare relazioni morganatiche con altri campi del sapere. Così, ad esempio, quando in occasione del “Joint Congress of Pure and Applied Mathematics” fu chiesto a David Hilbert di pronunciare un discorso che favorisse la caduta delle ostilità che si percepivano tra i due gruppi di matematici, egli iniziò con queste parole:
“Si dice spesso che la matematica pura e quella applicata siano reciprocamente ostili. Non è vero. La matematica pura e quella applicata non sono reciprocamente ostili. La matematica pura e quella applicata non sono mai state reciprocamente ostili. La matematica pura e quella applicata non saranno mai reciprocamente ostili. La matematica pura e quella applicata non possono essere reciprocamente ostili perché, di fatto, non hanno assolutamente nulla in comune”.
Nonostante la matematica pura ami rimanere pura e starsene del tutto separata dalle altre scienze, le altre scienze, specialmente la fisica, amano la matematica e cercano di “fraternizzare” con essa il più possibile.
Infatti, quasi tutte le branche della matematica pura sono state messe al lavoro per spiegare l’una o l’altra caratteristica dell’universo fisico. Ciò include anche teorie quali quelle dei gruppi astratti, dell’algebra delle funzioni non permutabili e della geometria non euclidea, che sono sempre state considerate le più pure e incapaci di qualsiasi applicazione pratica.
C’è comunque un ampio settore della matematica rimasto ancora del tutto inutile per qualsiasi scopo pratico ad eccezione di quello di stimolare la ginnastica mentale, e perciò può portare con onore la “corona della purezza”. E’ la cosiddetta “teoria dei numeri” (cioè dei numeri interi), uno dei più antichi ed intricati prodotti del pensiero matematico puro.
Sembrerà strano ma la teoria dei numeri, essendo il tipo di matematica più puro, sotto certi aspetti può essere chiamata una scienza empirica o addirittura sperimentale. Infatti, molte delle sue proposizioni sono state formulate come risultato di esperimenti su ciò che si può fare con i numeri, nello stesso modo in cui le leggi della fisica sono il risultato di esperimenti su ciò che si può fare con gli oggetti materiali. Come nella fisica, alcune proposizioni sono state provate “matematicamente”, mentre altre rimangono ancora di origine puramente empirica e continuano a sfidare i cervelli dei migliori matematici.
Prendiamo ad esempio il problema dei numeri primi, cioè dei numeri che non possono essere scritti come il prodotto di due o più numeri più piccoli. 1, 2, 3, 5, 7, 11, 13, 17, ecc. sono numeri primi, mentre 12, ad esempio, non lo è perché può essere scritto come 2 · 2 · 3.
Il numero dei numeri primi è infinito, oppure esiste il più grande numero primo oltre il quale ogni numero può essere rappresentato come il prodotto dei numeri primi che già possediamo? Questo problema fu affrontato per la prima volta da Euclide stesso, il quale fornì una semplice ed elegante prova che i numeri primi si estendono oltre ogni limite per cui non esiste qualcosa che si possa chiamare “il più grande numero primo”.
Per esaminare la questione supponiamo per un momento che ci sia un numero finito di numeri primi e che un certo numero che indichiamo con N sia il più grande numero primo. Ora prendiamo il prodotto di tutti i numeri primi noti e ad esso aggiungiamo 1. Possiamo scrivere così:
$$(1\cdot 2\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13\cdot\,\text{…}\cdot N)+1$$
Ne risulta un numero decisamente superiore al presunto “numero primo massimo”. Ne risulta anche che questo numero non può essere divisibile per nessuno dei numeri primi noti (fino ad $N$ incluso) dato che, dal modo in cui è stato costruito, la divisione per uno qualsiasi dei numeri primi noti darebbe come resto $1$.
Quindi il nostro numero deve essere un numero primo oppure deve essere divisibile per un numero primo maggiore di $N$. Entrambi i casi contraddicono l’assunzione iniziale e cioè che $N$ sia il più grande numero primo esistente.
La prova è per retuctio ad absurdum, uno degli strumenti preferiti dai matematici.
Una volta che sappiamo che il numero di primi è infinito ci chiediamo se esiste un modo semplice per elencarli senza saltarne nessuno. Il metodo per fare questo fu proposto dal filosofo e matematico greco Eratostene ed è conosciuto come il “crivello”.
Tutto quello che c’è da fare è scrivere la sequenza completa dei numeri interi, $1, 2, 3, 4, $ ecc. e poi cancellare dalla lista prima tutti i multipli di $2$, poi tutti i multipli di $3$, poi quelli di $5$, ecc.
Nel disegno qui a fianco è illustrato il crivello di Eratostene dei primi $100$ numeri interi. Contiene ventisei numeri primi. Usando questo semplice sistema del crivello sono state costruite tavole fino a un miliardo di numeri.
Però sarebbe molto più semplice se si trovasse una formula per mezzo della quale poter trovare rapidamente e automaticamente solo i numeri primi e tutti i numeri primi. Nonostante i tentativi fatti lungo i secoli una tale formula non si è ancora trovata.
Nel 1640 il famoso matematico francese Pierre de Fermat pensò di aver trovato una formula che produce solo numeri primi.
Nella sua formula,
$$2^{2^n}+1$$
$n$ indica un numero intero, $1, 2, 3, 4,$ ecc. Usando la formula otteniamo:
$2^2+1=5$
$2^{2^2}+1=17$
$2^{2^3}+1=257$
$2^{2^4}+1=65\,537$
Infatti, ognuno di questi numero è primo. Ma circa un secolo dopo dall’annuncio di Fermat, il matematico tedesco Eulero scoprì che il quinto calcolo di Fermat, $2^{2^5}+1$, il risultato, $4\,294\,967\,297$, è il prodotto di $6\,700\,417$ e $641$. Così fu provato che la regola empirica di Fermat era sbagliata.
Un’altra importante formula che produce molti numeri primi è:
$$n^2-n+41$$
nella quale $n$ è sempre un numero della successione naturale $1, 2, 3,$ ecc. Si è scoperto che con valori di $n$ compresi tra $1$ e $40$ la formula produce esclusivamente numeri primi ma sfortunatamente fallisce al quarantunesimo passaggio.
Infatti,
$41^2-41+41=41\cdot 41$
che è un numero quadrato, non un numero primo.
Un altro tentativo è stato questo:
$$n^2-79n+1601$$
La formula produce numeri primi per valori di $n$ fino a $79$ ma fallisce per il numero $80$!
Così il problema di trovare una formula generale che produca solo numeri primi è ancora irrisolto.
Un altro interessante esempio di un teorema della teoria dei numeri la cui correttezza non è ancora stata dimostrata è la cosiddetta congettura di Goldbach, proposta dal matematico prussiano nel 1742. Essa recita: “Ciascun numero pari può essere rappresentato come somma di due numeri primi“.
Si può facilmente verificare che la congettura è vera se applicata ad alcuni esempi, così:
$12 = 7 + 5$
$24 = 17 + 7$
$39 = 29 + 3$
Nonostante l’immensa quantità di lavoro fatto su questa congettura, i matematici non sono ancora riusciti a fornire una prova conclusiva della sua infallibilità o trovare un esempio che ne provi la falsità. Nel 1931 il matematico russo Schnirelman riuscì a salire il primo valido gradino verso l’agognata verifica. Fu in grado di dimostrare che ciascun numero pari è la somma di non più di $300\,000$ primi. Più recentemente si è ridotta la distanza tra la somma dei non più di trecentomila numeri primi e il desiderato traguardo della somma di due primi grazie ad un altro matematico russo, Vinogradov, il quale fu in grado di ridurla alla somma di quattro primi. Ma gli ultimi due gradini che separano i quattro di Vinogradoff dai due di Goldbach sembrano essere i più duri da superare e nessuno può affermare se ci vorranno solo pochi anni o alcuni secoli per provare la sua falsità o la correttezza della congettura.
Ebbene, sembriamo ancora molto lontani dalla scoperta di una formula che fornisca automaticamente tutti i numeri primi per quanto grandi essi siano, e non c’è nemmeno la sicurezza che tale formula possa mai essere scoperta.
Ora possiamo affrontare una domanda più umile, riguardo la percentuale di numeri primi che si possono trovare in un intervallo dato. Il numero di primi rimane approssimativamente costante se si considerano intervalli di numeri via via più grandi? Cresce o decresce? Possiamo tentare di risolvere il problema empiricamente, contando il numero di primi per diversi intervalli, come nella tavola seguente:
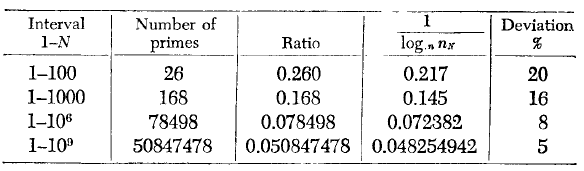
Si nota innanzitutto che il numero di primi decresce gradualmente con il crescere dell’intervallo considerato, ma che non si arriverà mai ad un punto in cui non ci saranno più numeri primi.
Esiste un modo semplice per rappresentare matematicamente questa diminuzione percentuale dei numeri primi tra i numeri grandi? Sì esiste, e la legge che governa la distribuzione media dei numeri primi rappresenta una delle più straordinarie scoperte dell’intera scienza matematica. La legge afferma, semplicemente, che la percentuale dei numeri primi compresi tra $1$ e $N$ è approssimativamente uguale al logaritmo naturale di $N$ (1). Più grande è $N$, migliore è l’approssimazione.
La quarta colonna della tabella contiene i logaritmi naturali di $N$. Se si confronta il loro valore con quello corrispondente della terza colonna si nota che l’accordo è tanto maggiore quanto più grande è $N$.
Come per molte altre proposizioni nella teoria dei numeri, anche il teorema dei numeri primi appena descritto è stato prima scoperto empiricamente e rimase per molto tempo senza essere confermato da una prova strettamente matematica. Solo verso la fine del diciannovesimo secolo il matematico francese Jacques Hadamard e il belga Charles Jean de la Vallée-Poussin riuscirono a dimostrarlo, con un metodo troppo complesso e difficile per essere spiegato qui.
L’argomento dei numeri interi non può essere abbandonato senza menzionare il famoso Grande Teorema di Fermat [o Ultimo teorema di Fermat] che servirà come un esempio di un tipo di problemi non necessariamente connessi con i numeri primi. Questo problema ha le sue radici nell’antico Egitto dove, ogni buon carpentiere sapeva che un triangolo con tre lati nella proporzione $3:4:5$ doveva contenere un angolo retto. Infatti gli egiziani usavano questo triangolo, conosciuto adesso con il nome di triangolo egiziano, come squadra per i lavori di carpenteria.(2)
Nel terzo secolo, Diofanto di Alessandria cominciò a chiedersi se il $3$ e il $4$ fossero gli unici numeri interi per i quali la somma dei loro quadrati fosse uguale al quadrato di un altro numero intero. Egli trovò che esistevano altre terne (in realtà un infinito numero di terne) di numeri che possiedono la stessa proprietà e fornì una regola generale per calcolarle. Questi triangoli rettangoli i cui lati hanno lunghezze che si possono esprimere con tre numeri interi sono noti attualmente come triangoli pitagorici e il triangolo egiziano è il primo di essi. Il problema della costruzione dei triangoli pitagorici può essere enunciato semplicemente come un’equazione algebrica nella quale $x, y$ e $z$ devono essere numeri interi:(3)
$$x^2+y^2=z^2$$
Nel 1621 il parigino Pierre Fermat acquistò una copia della recente traduzione in francese del libro di Diofanto Aritmetica, nel quale si discutono i triangoli pitagorici. Quando lo lesse, scrisse una piccola nota sul margine di una pagina con l’affermazione che, mentre $x^2+y^2=z^2$ possiede infinite soluzioni, qualsiasi equazione del tipo:
$$x^n+y^n=z^n$$
dove $n$ è un numero maggiore di $2$, non ha mai soluzioni.
“Di questo ho trovato una splendida dimostrazione – aggiunse Fermat – ma la ristrettezza del margine di questo libro non la può contenere.“.
Dopo la sua morte il libro di Diofanto fu scoperto nella sua libreria e la nota al margine divenne famosa in tutto il mondo. Ciò è avvenuto tre secoli fa e da allora i migliori matematici di ogni paese hanno tentato di ricostruire la dimostrazione che Fermat aveva in mente quando la scrisse. Ma fino ad ora nessuna dimostrazione è stata ancora trovata. Comunque sono stati fatti notevoli passi avanti e come conseguenza si è sviluppato un intero nuovo ramo della matematica, chiamato “teoria degli ideali”. Eulero dimostrò l’impossibilità di una soluzione intera alle equazioni $x^3+y^3=z^3$ e $x^4+y^4=z^4$; Dirichlet dimostrò la stessa cosa per $x^5+y^5=z^5$ e per mezzo degli sforzi coordinati di molti matematici ora siamo in grado di dimostrare che le equazioni di Fermat non hanno soluzioni per valori di $n$ minori di $269$. Ma non abbiamo ancora una dimostrazione generale, valida per qualsiasi valore dell’esponente $n$ ed è sempre più realistico il sospetto che Fermat stesso non fosse in possesso di questa dimostrazione, oppure che la dimostrazione contenesse un errore. Il problema divenne famoso soprattutto quando fu offerto un premio di centomila marchi tedeschi per la sua soluzione sebbene, ovviamente, tutti i tentativi degli amatoriali cacciatori di premi furono senza successo.
Naturalmente, rimane sempre la possibilità che il teorema sia sbagliato e che un giorno qualcuno trovi un esempio di una somma di due potenze intere di uguale esponente che danno come risultato la potenza di un numero intero con lo stesso esponente. Ma, da dato che per trovare questo esempio è necessario usare esponenti maggiori di $269$, la ricerca non è facile.[4]
Il logaritmo naturale si può esprimere come il prodotto tra il logaritmo decimale e il numero $2\text{,3026}$.
Il teorema di Pitagora, come lo si insegna nella scuola, è espresso in questo modo:
$$3^2+4^2=5^2$$
La regola generale di Diofanto afferma che se si prendono due numeri qualsiasi $a$ e $b$ tali che $2ab$ sia un quadrato perfetto,
$$x=a+\sqrt{2ab}$$
$$y=b+\sqrt{2ab}$$
$$z=a+b+\sqrt{2ab}$$
e quindi l’equazione $x^2+y^2=z^2$ è facile da verificare con l’algebra ordinaria. Con questa regola possiamo costruire una tavola di tutte le possibili soluzioni che comincia così:
$3^2+4^2=5^2$
$5^2+12^2=13^2$
$6^2+8^2=10^2$
$7^2+24^2=25^2$
$8^2+15^2=17^2$
$9^2+12^2=15^2$
$9^2+40^2=41^2$
$10^2+24^2=26^2$
(la prima terna è il triangolo egiziano)
[Ai tempi della pubblicazione del libro di Gamow la dimostrazione dell’ultimo teorema di Fermat non era stata ancora trovata. Nel 1994 il matematico Andew Wiles dimostrò il teorema ricevendo un premio di cinquantamila dollari. Wiles utilizzò elementi di algebra e matematica moderni che Fermat non avrebbe potuto conoscere. Quasi tutti i matematici sono dell’idea che Fermat si fosse sbagliato.]
—–
Capitolo precedente: Contare l’infinito
Capitolo successivo: la misteriosa radice di meno uno
Copyright © 2024 | MH Purity lite WordPress Theme by MH Themes
