La misteriosa radice di meno uno

Addentriamoci in una matematica un po’ più avanzata. Due per due fa quattro, tre per tre fa nove, quattro per quattro fa sedici e cinque per cinque fa venticinque. D’altra parte: la radice quadrata di quattro è due, la radice quadrata di nove è tre, la radice quadrata di sedici è quattro e la radice quadrata di venticinque è cinque.

Ma qual è la radice quadrata di un numero negativo?

Che significato hanno espressioni come $\sqrt{-5}$ e $\sqrt{-1}$?

Se si tenta di risolvere razionalmente la questione si arriva indubbiamente alla conclusione che queste espressioni non hanno alcun senso. Per citare le parole di Brahmin Bhaskara, un matematico del dodicesimo secolo:

“Il quadrato di un numero positivo e anche di un numero negativo, è positivo. Di conseguenza, la radice quadrata di un numero positivo è duplice, positiva e negativa. Non esiste la radice quadrata di un numero negativo perché un numero negativo non è un quadrato”.

Ma i matematici sono gente ostinata e, ogni volta che da una formula salta fuori qualcosa che sembra non avere senso, fanno di tutto per trovare un significato. E la radice quadrata dei numeri negativi continua ad uscir fuori da ogni angolo, dalle semplici questioni aritmetiche che occuparono i matematici del passato ai problemi di unificazione dello spazio e del tempo nella cornice della teoria della relatività.

L’uomo coraggioso che per primo scrisse sulla carta una formula che includeva l’apparentemente insensata radice di un numero negativo fu Cardano, un matematico italiano del sedicesimo secolo. Discutendo la possibilità di dissociare il numero 10 in due parti tali che il loro prodotto fosse 40, mostrò che, nonostante il suo problema non avesse nessuna soluzione razionale, si poteva fornire la risposta nella forma di due espressioni matematiche:(1)

$5+\sqrt{-15}$
e
$5-\sqrt{-15}$

Cardano scrisse queste righe con la riserva che esse erano prive di significato, fittizie e immaginarie, ma le scrisse comunque:

E se qualcuno osa scrivere radici quadrate di numeri negativi, sebbene immaginarie, il problema della dissociazione del numero dieci nelle due parti desiderate diventa risolvibile.

Una volta rotto il ghiaccio le radici quadrate dei numeri negativi, chiamati in seguito numeri immaginari come Cardano stesso li apostrofò, furono usate da vari matematici sempre più spesso, sebbene con grandi riserve e con le dovute scuse.
Nel libro sull’algebra del famoso matematico tedesco Eulero (Vollständige Anleitung zur Algebra, 1770) troviamo ormai numerose applicazioni dei numeri immaginari, mitigate comunque dal commento:

“Tutte le espressioni come $\sqrt{-1}$ oppure $\sqrt{-}2$, ecc., sono numeri impossibili o immaginari, dato che rappresentano radici di quantità negative, e di tali numeri possiamo certamente affermare che non sono nulla, e nemmeno maggiori di nulla, e nemmeno minori di nulla, e ciò li rende necessariamente immaginari o impossibili”.

Nonostante tutti questi abusi e queste scuse i numeri immaginari diventano presto inevitabili in matematica, allo stesso modo delle frazioni o dei radicali, e senza usarli non si arriverebbe da nessuna parte.

La famiglia dei numeri immaginari rappresenta, come dire, un’immagine speculare fittizia degli ordinari numeri reali e, esattamente allo stesso modo in cui si possono produrre tutti i numeri reali partendo dall’unità, si possono costruire tutti i numeri immaginari partendo dall’unità immaginaria $\sqrt{-1}$ che viene indicata normalmente dal simbolo $i$.

E’ facile vedere che:

$\sqrt{-9}=\sqrt{9}\cdot\sqrt{-1}=3i$
$\sqrt{-7}=\sqrt{7}\cdot\sqrt{-1}=2\text{,646…}\cdot i$, ecc.

così ogni numero reale ha il suo compagno immaginario. Si possono combinare numeri reali e immaginari costruendo espressioni come:

$5+\sqrt{-15}=5+i\sqrt{15}$

come fece per la prima volta Cardano. Queste forme ibride sono note come numeri complessi.

Per ben due secoli dopo l’entrata dei numeri immaginari nella matematica, essi rimasero avvolti da un velo di mistero e di incredulità finché non ottennero una interpretazione geometrica da parte di due matematici amatoriali: l’agrimensore norvegese Caspar Wessel e il contabile parigino Robert Argand.

Secondo la loro interpretazione un numero complesso, ad esempio $3+4i$, può essere rappresentato come in figura, dove $3$ corrisponde alla distanza orizzontale e $4$ a quella verticale:

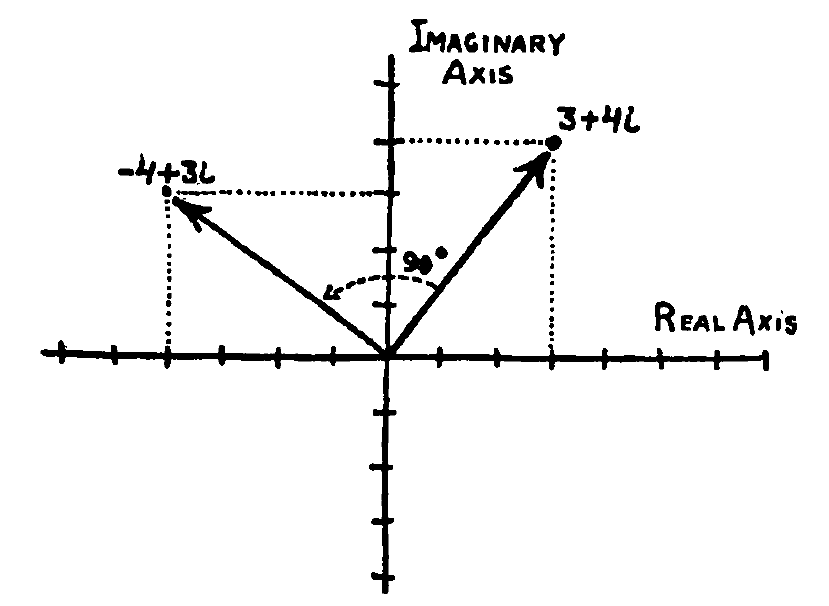
Tutti i numeri reali si possono rappresentare come punti dell’asse delle ascisse mentre tutti i numeri immaginari come punti dell’asse delle ordinate. Se si moltiplica un numero reale, ad esempio $3$, che rappresenta un punto dell’asse delle ascisse, per l’unità immaginaria $i$, che invece si trova sull’asse delle ordinate, si ottiene il numero puramente immaginario $3i$, che va disegnato anch’esso sull’asse verticale. Perciò, la moltiplicazione per $i$ è geometricamente equivalente ad una rotazione antioraria di $90^\circ$.

Se ora si moltiplica $3i$ ancora una volta per $i$, dobbiamo ruotarlo ancora di $90^\circ$ e il risultato si trova ancora sull’asse orizzontale, ma nella sua parte negativa. Così:

$3i\cdot i=3i^2=-3$

oppure:

$i^2=-1$

La frase “il quadrato di $i$ è uguale a $-1$” è molto più comprensibile che la frase “ruotando due volte di un angolo retto, sempre in senso antiorario, ti ritroverai girato verso la direzione opposta”.

La stessa regola si può applicare, ovviamente, anche ai numeri complessi. Moltiplicando $3+4i$ per $i$ si ottiene:

$(3+4i)i=3i+4i^2=3i-4=-4+3i$

E, come si può vedere subito dalla figura, il punto $-4+3i$ corrisponde al punto $3+4i$ ruotato di $90^\circ$ in senso antiorario rispetto all’origine degli assi. Così, la moltiplicazione per $-i$ non è nient’altro che una rotazione oraria attorno all’origine.

Se continuate ancora a sentire un velo di mistero che avvolge i numeri immaginari, sarete in grado di toglierlo definitivamente risolvendo un semplice problema in cui i numeri immaginari trovano un’applicazione pratica.

C’era un uomo giovane e avventuroso che scoprì tra le carte di suo nonno un pezzo di pergamena che rivelava il luogo di un tesoro nascosto. Nelle istruzioni si leggeva:

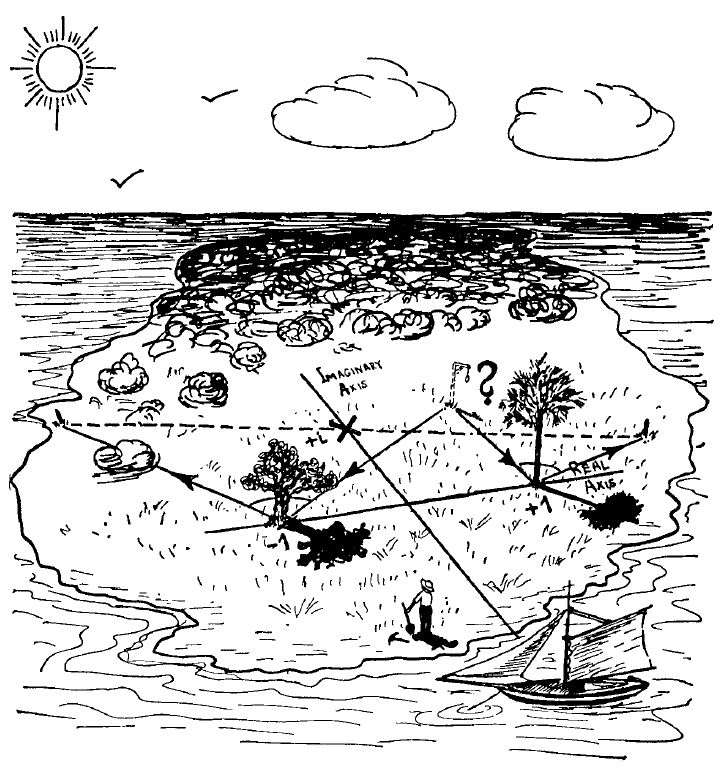
“Fai vela verso …….. di latitudine nord e ………. di longitudine ovest (2) dove troverai un’isola deserta. Nella parte nord, presso una quercia solitaria e un pino solitario (3), troverai un grande prato non recintato. Là troverai anche una forca dove un tempo si impiccavano i traditori. Parti dalla forca e vai verso la quercia contando i tuoi passi. Giunto alla quercia, gira a destra ad angolo retto e fai lo stesso numero di passi. Qui pianta un paletto nel terreno. Ora devi tornare alla forca e camminare verso il pino, contando i tuoi passi. Arrivato al pino gira a sinistra ad angolo retto, fai un uguale numero di passi e pianta un altro paletto. Scava a metà strada tra i due paletti: il tesoro si trova là”

Le istruzioni erano chiare ed esplicite così il nostro giovane noleggiò una nave e fece vela verso i mari del sud. Trovò l’isola, il prato, la quercia e il pino ma, con suo grande dispiacere, la forca non c’era più. Era passato troppo tempo da quando il documento era stato scritto; la pioggia, il sole e il vento avevano disintegrato il legno e trasformato la forca in terriccio, senza lasciare alcuna traccia.

Il nostro giovane avventuroso cadde in disperazione e in rabbiosa frenesia cominciò a scavare a casaccio tutto intorno al prato. Ma i suoi sforzi furono inutili: l’isola era troppo grande! Così tornò indietro a mani vuote e il tesoro probabilmente si trova ancora là.

E’ una storia triste, ma ancora più triste è il fatto che il giovane avrebbe potuto trovare il tesoro se solo avesse avuto qualche conoscenza di matematica e, in particolare, sull’uso dei numeri immaginari. Vediamo se noi riusciamo a trovare il tesoro anche se, per lui, è ormai troppo tardi.

Consideriamo l’isola come un piano di numeri complessi. Tracciamo l’asse dei numeri reali tra le basi dei due alberi e l’asse immaginario perpendicolare a questo e passante per il punto medio tra i due alberi. Prendendo come unità di misura la metà della distanza tra gli alberi possiamo dire che la quercia si trova nel punto $-1$ dell’asse reale e il pino al punto $+1$. Non conosciamo il punto in cui si trovava la forca, perciò indichiamo la sua posizione ipotetica con la lettera greca $\Gamma$ (gamma maiuscolo) che assomiglia ad una forca. Dato che la forca non si trovava necessariamente su uno dei due assi, il punto $\Gamma$ può essere considerato un numero complesso:

$$\Gamma=a+bi$$

in cui il significato di $a$ e $b$ è evidente nella figura.

Eseguiamo ora alcuni calcoli ricordando le regole della moltiplicazione dei numeri complessi descritta sopra. Se la forca è in $\Gamma$ e la quercia in $-1$, la loro separazione in distanza e direzione si può esprimere con:

$$(-1)-\Gamma = -(1+\Gamma)$$

Allo stesso modo, la separazione tra la forca e il pino si può esprimere come:

$$1-\Gamma$$

Per ruotare queste due distanze di $90^\circ$ in senso orario (verso destra) e in senso antiorario (verso sinistra), dobbiamo moltiplicarle per $-i$ e per $i$ e così troviamo le posizioni dei due paletti che saranno le seguenti:

primo paletto: $(-i)[-(1+\Gamma)]+1=i(\Gamma+1)-1$

secondo paletto: $(+i)(1-\Gamma)-1=i(1-\Gamma)+1$

Dato che il tesoro è a metà strada tra i due paletti, possiamo calcolare la semisomma di questi due numeri complessi:

$$\frac{[i(\Gamma+1)-1+i(1-\Gamma)+1]}{2} = \frac{[+i\Gamma+i-1+i-i\Gamma+1]}{2} = \frac{(+2i)}{2} = +i$$

Ora sappiamo che la posizione della forca, indicata da $\Gamma$, è scomparsa da qualche parte durante i calcoli e che, senza preoccuparci di dove essa sia, il tesoro deve per forza trovarsi alla posizione $+i$. Così, se il nostro giovane coraggioso avesse potuto fare questi semplici calcoli matematici, non avrebbe tentato di scavare l’intera isola ma sarebbe andato subito nel punto indicato dalla croce e lì avrebbe trovato il tesoro.

Se non siete ancora convinti che non è necessario conoscere la posizione della forca per trovare il tesoro, segnate su un foglio la posizione dei due alberi e seguite le istruzioni della pergamena scegliendo a caso alcune posizioni possibili della forca. Arriverete sempre alla stessa posizione del tesoro, corrispondente alla posizione $+i$ del piano complesso!

[vedi: Simulazione geogebra del problema del tesoro nascosto nel piano complesso. Trascinando la FORCA, la QUERCIA o il PINO in qualsiasi punto del piano, la posizione del TESORO è sempre sull’asse immaginario a distanza unitaria +i dall’origine]

Un altro tesoro nascosto che è stato trovato usando la radice quadrata di $-1$ è stata la sorprendente scoperta che il nostro spazio tridimensionale e il tempo possono essere unificati in una rappresentazione a quattro dimensioni, governata dalle regole della geometria a quattro dimensioni. Ma torneremo su questa scoperta in uno dei prossimi capitoli nei quali discuteremo le idee di Albert Einstein e la sua teoria della relatività.

1)Ecco la dimostrazione:

$(5+\sqrt{-15})+(5-\sqrt{-15})\,=\,5+5\,=\,10$

$(5+\sqrt{-15})\times(5-\sqrt{-15})=$
$=(5\times 5)+5\sqrt{-15}-5\sqrt{-15}-(\sqrt{-15}\times\sqrt{-15})=$
$=(5\times 5)-(-15)=25+15\,=\,40$

(2) I valori di longitudine e latitudine erano scritti nel documento ma sono stati omessi in questo testo, per non rivelare il segreto.

(3) I nomi degli alberi sono stati cambiati per le ragioni descritte sopra. Ovviamente in un’isola del tesoro tropicale ci sono altre varietà di alberi.

—–

Capitolo precedente: La matematica più pura

Capitolo successivo: Proprietà inconsuete dello spazio

Fogli sparsi

di Nicola Scarpel ¤

La misteriosa radice di meno uno