• Miriadi di granelli di sabbia e di chicchi di frumento
• Storia della fine del mondo
• Una stampante “universale”
• Come contare l’infinito
• La matematica più pura
• La misteriosa radice di meno uno
• Proprietà inconsuete dello spazio
• Geometria senza misure
• Rovesciare lo spazio
• Il tempo è la quarta dimensione

L’idea di quarta dimensione è spesso circondata da un alone di mistero e di sospetto. Come osiamo noi, creature di lunghezza, altezza e spessore, parlare dello spazio a quattro dimensioni? Usando tutta la nostra intelligenza tridimensionale è possibile immaginare un “superspazio” o meglio un iperspazio di quattro dimensioni? E come potrebbero essere un cubo o una sfera quadridimensionali? Quando diciamo di “immaginare” un drago gigante con una lunga coda squamata e con le fiamme che escono dalle narici, oppure un super aereo di linea con una piscina e un paio di campi da tennis sulle sue ali, in realtà stiamo delineando un’immagine mentale di come sarebbero queste cose se ci apparissero improvvisamente davanti agli occhi. E questa immagine la disegniamo nello sfondo del familiare spazio a tre dimensioni nel quale sono situati tutti i comuni oggetti, compresi noi stessi. Se è questo il significato della parole “immaginare”, allora è possibile immaginare una figura a quattro dimensioni nello sfondo del comune spazio tridimensionale, allo stesso modo in cui è possibile schiacciare un corpo tridimensionale su un piano.

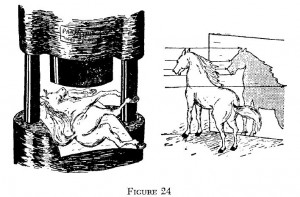
Ma, aspettate un momento. In un certo senso, noi siamo in grado di appiattire i corpi tridimensionali sul piano, disegnandoli. In questi casi, comunque, non dobbiamo utilizzare una pressa idraulica o qualche tipo di forza fisica per eseguire tale operazione, semmai dobbiamo applicare il metodo noto come “proiezione”.

La differenza tra i due modi di schiacciare un corpo su un piano (ad esempio un cavallo) può essere compresa immediatamente guardando la figura 24.

Per mezzo di un’analogia, ora possiamo affermare che pur non essendo possibile “schiacciare” un corpo quadridimensionale in uno spazio tridimensionale senza che alcune parti schizzino via, è invece possibile eseguire delle “proiezioni” di varie figure a quattro dimensioni nel nostro spazio a tre dimensioni. Dobbiamo ricordare però che allo stesso modo in cui la proiezione sul piano di un oggetto tridimensionale è una figura piana a due dimensioni, la proiezione di un “supercorpo” di quattro dimensioni nel nostro spazio ordinario sarà rappresentata da una figura a tre dimensioni.

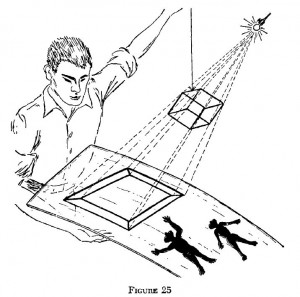
Per chiarire meglio la questione, proviamo a pensare in che modo le creature-ombra bidimensionali che vivono su una superficie potrebbero concepire l’idea di un cubo tridimensionale. Possiamo facilmente immaginarlo, dato che rispetto a loro, noi siamo degli esseri superiori, a tre dimensioni, e possiamo guardare il mondo bidimensionale dall’alto, cioè da una terza direzione. L’unico modo per schiacciare un cubo su un piano è quello di proiettarlo con il metodo mostrato nella figura 25.

Osservando questa proiezione e varie altre proiezioni che si possono ottenere facendo ruotare il cubo originale, i nostri amici bidimensionali potrebbero farsi almeno un’idea su alcune proprietà della misteriosa figura chiamata “un cubo tridimensionale”. Non potranno mai “saltare fuori” dalla loro superficie e visualizzare il cubo nel modo in cui lo vediamo noi, ma osservando semplicemente la proiezione saranno in grado di dire, ad esempio, che il cubo possiede otto vertici e dodici spigoli.

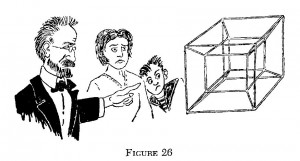
Se ora osserviamo la figura 26 ci troveremo esattamente nella situazione della povera creatura-ombra bidimensionale che esamina la proiezione di un cubo sulla loro superficie. In realtà, la strana struttura complessa osservata con grande stupore dai membri della famiglia, è una proiezione di un “supercubo”, o meglio un “ipercubo” quadridimensionale nel nostro ordinario spazio tridimensionale. (1)

Se si esamina con attenzione questa figura si riconosceranno facilmente le stesse enigmatiche caratteristiche osservate dalle creature-ombra della figura 25: mentre la proiezione di un cubo ordinario sul piano è rappresentato da due quadrati, uno dentro l’altro e connessi per i vertici, la proiezione di un ipercubo nello spazio ordinario è formato da due cubi, uno dentro l’altro. Si possono facilmente contare 16 vertici, 32 spigoli e 24 facce. Proprio un bel cubo no?

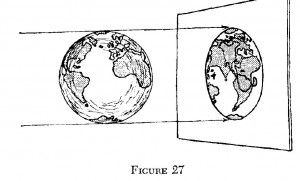
Ora vediamo come potrebbe apparire una sfera a quattro dimensioni. Lo facciamo nel modo che ci è più familiare, quello della proiezione di una sfera ordinaria sulla superficie piana. Pensiamo ad esempio da un globo terrestre trasparente, con i continenti e gli oceani disegnati sulla sua superficie, proiettato su un muro (figura 27).

Sul muro i due emisferi si sovrappongono e, giudicando dalla proiezione, si potrebbe pensare che la distanza tra New York e Pechino sia molto piccola. Ma è solo una impressione. In realtà ogni punto della proiezione rappresenta due punti opposti sul globo e la proiezione di un aereo che vola da New York alla Cina si muoverà fino al bordo della proiezione piana e poi tornerà indietro. Nonostante le proiezioni delle traiettorie di due aerei diversi potrebbero intersecarsi sulla proiezione, non avverrebbe nessuna collisione sul globo dato che essi si troverebbero in due posizioni opposte.

Queste sono le proprietà di una sfera ordinaria. Spingendo un po’ oltre la nostra immaginazione non avremo difficoltà di vedere come potrebbe apparire la proiezione nello spazio ordinario di una “ipersfera”. Allo stesso modo in cui la proiezione piana di una sfera ordinaria è formata da due dischi piatti sovrapposti punto a punto e uniti lungo la circonferenza esterna, la proiezione nello spazio di una ipersfera deve essere immaginata come due corpi sferici sovrapposti e uniti lungo le loro superfici esterne. Nel capitolo precedente abbiamo già discusso una struttura straordinaria come questa, come l’esempio di una forma tridimensionale chiusa analoga ad una superficie sferica. Così, tutto quello che dobbiamo aggiungere qui è che la proiezione tridimensionale di una sfera a quattro dimensioni non è nient’altro che la coppia di mele gemelle siamesi già descritte, formate da due normali mele che sono cresciute assieme lungo la superficie della loro buccia.

Allo stesso modo, con il metodo dell’analogia, possiamo rispondere a molte altre domande concernenti le proprietà delle figure a quattro dimensioni sebbene, per quanto ci proviamo, non riusciamo mai ad immaginare nel nostro spazio fisico una quarta direzione indipendente.

Ma si ci pensiamo un po’ di più, scopriamo che per concepire la quarta dimensione non è per niente necessario diventare dei mistici. Esiste una parola che molti di noi usano ogni giorno per designare ciò che potrebbe, e in realtà dovrebbe, essere considerata una quarta direzione indipendente nel mondo fisico. Intendiamo il tempo che, assieme allo spazio, è usato comunemente per descrivere gli eventi che accadono attorno a noi. Quando parliamo di qualsiasi evento dell’universo, sia che si tratti di un incontro casuale con un amico per la strada o dell’esplosione di una lontana stella, noi non diciamo soltanto dove esso accade, ma anche quando. Così aggiungiamo un fatto ulteriore, una data, ai tre fatti direzionali tipici della localizzazione di un posto.

Se si analizza ulteriormente l’argomento, si realizzerà facilmente che ogni oggetto fisico possiede quattro dimensioni, tre nello spazio e una nel tempo. Così la casa nella quale viviamo si estende in larghezza, lunghezza, altezza e tempo e l’ultima estensione è misurata dal momento in cui la casa è stata costruita fino alla data in cui brucerà oppure sarà abbattuta da qualche ditta, o crollerà per età avanzata.

La direzione del tempo non è la stessa delle tre direzioni dello spazio. Gli intervalli di tempo sono misurati dall’orologio, il cui il tic-tac denota i secondi e il din-don indica le ore; gli intervalli di tempo invece sono misurati con il righello. Se per misurare la larghezza, la lunghezza e l’altezza si può usare un righello, non si può mettere lo stesso righello sull’orologio per misurare la durata del tempo. Inoltre, mentre con il righello si può misurare lo spazio spostandolo in avanti, a destra o verso l’alto, e poi tornare anche indietro, con il tempo non si può tornare indietro e siamo costretti ad andare forzatamente dal passato al futuro.

Una volta chiarite queste differenze tra la direzione del tempo e le tre direzioni nello spazio, possiamo ancora usare il tempo come quarta direzione nel mondo degli eventi fisici, senza però dimenticare che non è esattamente la stessa cosa.

Scegliendo il tempo come quarta dimensione sarà molto più facile visualizzare le immagini a quattro dimensioni discusse all’inizio di questo capitolo. Ad esempio, ricordate la strana figura della proiezione del cubo a quattro dimensioni? 16 vertici, 32 spigoli e 24 lati! Non c’è da stupirsi se i personaggi della figura 26 guardano sorpresi questo mostro geometrico.

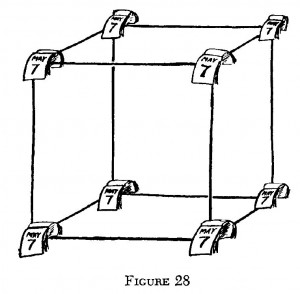
Dal nostro nuovo punto di vista, comunque, un cubo a quattro dimensioni è un cubo ordinario che esiste per un certo periodo di tempo. Supponiamo di costruire un cubo usando 12 asticelle di ferro il primo di maggio, e di smontarlo un mese dopo. Ogni vertice di questo cubo deve essere immaginato come una linea che si estende nella direzione del tempo per una lunghezza pari a un mese. Si potrebbe attaccare un piccolo calendario a ciascun vertice e sfogliare le pagine ogni giorno per mostrare la progressione nel tempo (figura 28).

Ora è facile contare il numero di spigoli nella nostra figura a quattro dimensioni. Abbiamo, di fatto, 12 spigoli spaziali all’inizio della sua esistenza, 8 spigoli temporali che rappresentano la durata di ciascun vertice, e di nuovo 12 spigoli spaziali alla fine della sua esistenza (2). In tutto fanno 32 spigoli.

In modo simile, possiamo contare i 16 vertici: otto vertici spaziali il 7 maggio e di nuovo gli stessi 8 vertici spaziali il 7 giugno. Lasciamo contare in modo simile, come esercizio per il lettore, il numero di facce della nostra figura a quattro dimensioni. Facendolo, si ricordi che alcune di queste facce saranno le normali facce del cubo originario, mentre le altre saranno facce “metà spaziali e per metà temporali” formate dagli spigoli originali del nostro cubo esteso nel tempo dal 7 maggio al 7 giugno.

Ciò che abbiamo detto a proposito del cubo a quattro dimensioni, può essere applicato a qualsiasi figura geometrica o ad ogni altro oggetto materiale attuale o passato.

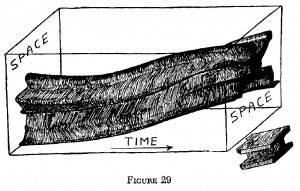
In particolare, proviamo a pensarci come una figura a quattro dimensioni, una specie di lunga barra di gomma che si estende nel tempo dal momento della nascita fino alla fine della nostra vita. Sfortunatamente non è possibile disegnare oggetti quadridimensionali sulla carta, perciò nella figura 29 abbiamo tentato di suggerire questa idea per mezzo dell’esempio di un uomo-ombra bidimensionale mettendo, al posto della direzione perpendicolare al piano dell’uomo-ombra, la direzione del tempo.

L’immagine rappresenta solo una piccola sezione della vita del nostro uomo-ombra. L’intera vita dovrebbe essere rappresentata da un barra molto più lunga, piuttosto sottile all’inizio, quando l’uomo è ancora un bambino, e che serpeggia per molti anni fino a raggiungere una forma costante al momento della morte (perché i morti non si muovono), e poi comincia a disintegrarsi.

Per essere più esatti, dobbiamo dire che questa barra quadridimensionale è formata da un gran numero di fasci separati di fibre, ciascuna composta da un singolo atomo. Nel coro della vita, molte di queste fibre stanno assieme in un fascio; solo alcuni di esse si separano, come ad esempio quando ci si taglia i capelli e le unghie. Dato che gli atomi sono indistruttibili, la disintegrazione del corpo umano dopo la morte dovrebbe essere in realtà considerata come la separazione dei filamenti in tutte le direzioni, ad eccezione forse di quelli che formano le ossa.

Nel linguaggio della geometria dello spazio-tempo a quattro dimensioni, la linea che rappresenta la storia di ogni particella materiale di ciascun individuo è chiamata “linea di mondo” [“Linea di universo” o “linea oraria”]. In modo simile, possiamo parlare di un gruppo di linee di mondo che formano un corpo composto.

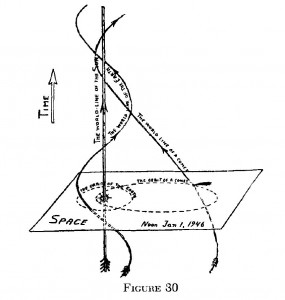
La figura 30 è un esempio astronomico delle linee di mondo del Sole, della Terra e di una cometa (3).

Come nell’esempio dell’uomo che salta, qui prendiamo uno spazio bidimensionale, il piano dell’orbita terrestre, e disponiamo l’asse del tempo perpendicolarmente ad esso. La linea di mondo del Sole è rappresentata in questo grafico dalla linea parallela all’asse del tempo, dato che consideriamo il Sole come immobile (4).

La linea di mondo della Terra, che ruota in un’orbita quasi circolare, è una spirale che si avvolge attorno alla linea del Sole, mentre la linea di mondo di una cometa si avvicina al Sole e poi se ne allontana di nuovo.

Vediamo che dal punto di vista della geometria spazio temporale a quattro dimensioni la topografia e la storia dell’universo si fondono in una immagine armoniosa, e tutto ciò che dobbiamo considerare è un intricato fascio delle linee di mondo che rappresentano il moto di singoli atomi, di animali o di stelle.

Note

 (1) Per essere precisi, la figura 26 mostra la proiezione nel piano del foglio di una proiezione nello spazio ordinario di un ipercubo.

 (2) Se non lo si capisce, si pensi ad un quadrato con quattro vertici e quattro lati che viene spostato ad una certa distanza perpendicolarmente alla sua superficie (nella terza direzione) per una distanza uguale ai suoi lati.

 (3) A dire il vero in questo caso si dovrebbe parlare di “nastri di mondo”, ma dal punto di vista astronomico si possono considerare le stelle e i pianeti come dei punti.

 (4) In realtà il nostro Sole si muove rispetto alle stelle in modo che, in riferimento al sistema stellare la linea di mondo del Sole dovrebbe essere in qualche modo inclinata da un lato.

Capitolo precedente: Rovesciare lo spazio