• Miriadi di granelli di sabbia e di chicchi di frumento
• Storia della fine del mondo
• Una stampante “universale”
• Come contare l’infinito
• La matematica più pura
• La misteriosa radice di meno uno
• Proprietà inconsuete dello spazio
• Geometria senza misure
• Rovesciare lo spazio
• Il tempo è la quarta dimensione

Abbiamo discusso le proprietà topologiche di superfici che sono esclusivamente a due dimensioni, ma è chiaro che simili questioni si possono discutere anche riguardo allo spazio tridimensionale nel quale viviamo. Perciò, una generalizzazione tridimensionale del problema della colorazione delle carte geografiche si può formulare così: ci viene chiesto di costruire un mosaico spaziale utilizzando dei pezzi di forma varia e di materiale diverso facendo in modo che non ci siano due pezzi dello stesso materiale a contatto tra loro. Quanti materiali diversi sono necessari?

Qual è l’analogia tridimensionale al problema dei colori sulla superficie dei una sfera o di un toro? E’ possibile pensare a qualche tipo inusuale di spazio a tre dimensioni che stia nella stessa relazione con il nostro spazio ordinario allo stesso modo in cui la sfera o il toro stanno in relazione con la superficie piana? Sulle prime, questa domanda sembra senza senso. Infatti, mentre possiamo facilmente immaginare superfici di varie forme, siamo inclini a credere che ci sia un solo tipo di spazio tridimensionale, cioè lo spazio fisico che ci è familiare e nel quale viviamo. Ma questa idea rappresenta una pericolosa delusione. Se stimoliamo un pochino la nostra immaginazione possiamo pensare ad uno spazio a tre dimensioni molto diverso da quello che si studia nei libri di testo che trattano la geometria euclidea.

La difficoltà nell’immaginare uno spazio così strano è dovuta soprattutto al fatto che noi stessi, in quanto creature tridimensionali, guardiamo lo spazio “dal di dentro” e non “dal di fuori” come invece facciamo quando abbiamo a che fare con superfici di forma strana. Ma con un po’ di ginnastica mentale possiamo immaginare anche questi strani spazi senza troppa fatica.

Iniziamo con il costruire un modello di spazio a tre dimensioni che dovrebbe avere proprietà simili a quelle della superficie di una sfera. La principale proprietà di una superficie sferica è che, pur non avendo confini, possiede un’area finita; semplicemente si incurva e si rinchiude su se stessa. Possiamo immaginare uno spazio tridimensionale che si chiude su se stesso in modo simile, così da avere un volume finito pur essendo privo di bordi spigolosi? Pensiamo a due corpi sferici, ciascuno limitato da una superficie sferica, come una mela è limitata dalla sua buccia.

Immaginiamo ora che questi due corpi sferici siano “uno dentro all’altro” ed aventi una superficie esterna in comune. Ovviamente non vi suggeriamo di prendere due corpi fisici reali, come due mele, e schiacciarle l’una con l’altra in modo che le loro bucce si incollino tra loro. Le mele si spremerebbero ma non potrebbero compenetrarsi.

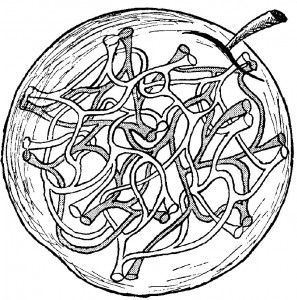
Si dovrebbe pensare piuttosto ad una mela con un intricato sistema di gallerie scavate da un verme. Anzi, ci dovrebbero essere due razze di vermi, diciamo una bianca e una nera, che non si sopportano a vicenda, che non si vogliono incontrare mai e che non fanno mai confluire le gallerie degli uni con le gallerie degli altri dentro alla mela, sebbene le aperture si trovino in punti adiacenti della stessa superficie. Una mela attaccata da queste due razze di vermi sembrerà, alla fine, qualcosa di simile alla figura 1: due reti di gallerie, strettamente intrecciate tra loro, che riempiono completamente l’interno della nostra mela. Nonostante le gallerie nere e quelle bianche passino molto vicine tra loro, l’unico modo per uscire dalla metà del labirinto ed entrare nell’altra metà è quella di raggiungere la superficie. Immaginiamo ora che le gallerie diventino via via più sottili e che diventino sempre più numerose e lunghe, alla fine possiamo raffigurarci lo spazio dentro alla mela come uno spazio formato da due spazi indipendenti e connessi soltanto da una superficie comune.

Se non vi piacciono i vermi, potete pensare ad un doppio sistema di corridoi e scalinate che potrebbe essere costruito dentro una gigantesca sfera, all’ultima Fiera Mondiale di New York. Si può pensare che ogni sistema di scalinate percorra l’intero volume della sfera ma, per passare da un certo punto del primo sistema al punto adiacente del secondo, sia necessario uscire completamente in superficie e ritornare giù di nuovo imboccando un’apertura del secondo sistema. Diciamo che le due sfere si sovrappongono senza interferire tra loro e un vostro amico potrebbe essere molto vicino a voi nonostante il fatto che, per incontrarlo e stringergli la mano, richiederebbe un lungo viaggio. È importante notare che tutti i punti di contatto dei due sistemi di scale non sono diversi da qualsiasi altro punto interno alla sfera, dato che dovrebbe essere possibile deformare l’intera struttura in modo che i punti di contatto vengano spinti verso l’interno e i punti che si trovano all’interno possano essere spinti verso la superficie. Il secondo punto importante di questo modello è che, nonostante la somma di tutte le lunghezze dei corridoi sia finita, non esiste nessun “vicolo cieco”. Ci possiamo muovere sempre attraverso tutti i corridoi e le scale senza mai essere fermati da mura o recinti e se cominciamo a camminare e continuiamo abbastanza a lungo, possiamo sempre, prima o poi, ritrovaci al punto di partenza. Osservando l’intera struttura “dal di fuori” uno potrebbe dire che una persona che si sta muovendo attraverso il labirinto, alla fine si ritroverà al punto di partenza semplicemente perché i corridoi girano sempre attorno, pur in modo graduale; a chi invece si trova “all’interno” e non può nemmeno sapere che esiste un “fuori”, lo spazio dovrebbe apparire di dimensioni “finite” pur essendo “senza confini”. Come vedremo in uno dei prossimi capitoli, questo “spazio tridimensionale chiuso in se stesso” che non possiede evidenti confini pur non essendo infinito è stato molto utile nella discussione sulle proprietà dell’universo nel suo insieme. Infatti, le osservazioni portate agli estremi limiti delle capacità dei telescopi, sembrano indicare che, a queste gigantesche distanze, lo spazio cominci a incurvarsi mostrando una pronunciata tendenza a tornare indietro e a chiudersi su se stesso nello stesso modo delle gallerie nel nostro esempio della mela mangiata dai vermi. Ma prima di spingerci oltre su questi interessanti problemi, dobbiamo imparare qualcosa di più su altre proprietà dello spazio.

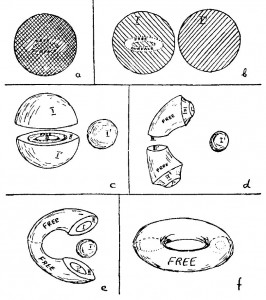
Non abbiamo ancora del tutto finito con la mela e i vermi, e la prossima domanda è se sia possibile trasformare una mela mangiata dai vermi in una ciambella. Certamente non intendiamo farla diventare gustosa come una ciambella, ma vogliamo fare in modo che sembri una ciambella. Stiamo discutendo di geometria e non di arte culinaria. Prendiamo una doppia mela come quella di cui abbiamo discusso, cioè due mele fresche messe “una dentro all’altra” e “incollate assieme” lungo le loro superfici. Immaginiamo che un verme abbia mangiato l’interno di una delle mele scavando un’unica larga galleria come si vede in figura 2. Si intende “l’interno di una delle mele” nel senso che al di fuori di quella galleria ciascun punto appartiene ad entrambe le mele, mentre all’interno della galleria c’è solo la sostanza dell’altra mela, quella non ancora mangiata dai vermi. Ora la nostra “doppia mela” possiede una superficie libera composta dalle pareti interne della galleria (figura 2, a). Riusciamo ad immaginare di deformare questa mela guasta in modo da trasformarla in una ciambella? Si assume, ovviamente, che il materiale di cui sia fatta la mela sia abbastanza plastico da poterlo rimodellare a piacere e che l’unica condizione sia quella che non si possa rompere in nessun punto. Per facilitare l’operazione, possiamo permetterci di tagliare il materiale della mela, a patto di incollarlo successivamente dopo che la deformazione sia completata.

Cominciamo separando del due bucce che formano la “doppia mela” (figura 2, b). Numeriamo le due superfici con I e I’, in modo da tenerne traccia durante le operazioni seguenti e quindi poterle incollare tra loro nuovamente quando avremo finito. Ora tagliamo la parte contenente la galleria in modo tale che il taglio attraversi tutta la galleria (figura 2, c). Questa operazione apre due nuove superfici tagliate che indicheremo con II, II’ e III, III’, in modo da sapere esattamente come unirle in seguito. Otteniamo così le superfici libere della galleria che sono destinate a diventare la superficie libera della ciambella. Ora prendiamo le parti tagliate e deformiamole nel modo indicato nella figura 2, d. La superficie libera viene stirata notevolmente verso l’esterno (in accordo con l’assunto che il materiale sia perfettamente plastico!). Al contrario, le superfici tagliate I, II e III sono state ridotte. Mentre stiamo operando sulla prima metà della “doppia mela”, dobbiamo anche pensare di ridurre le dimensioni della seconda metà, facendola diventare piccola come una ciliegia. Ora siamo pronti per incollare di nuovo le parti che erano state tagliate. Prima di tutto, e questo è facile, uniamo di nuovo le superfici III e III’ in modo da ottenere la forma mostrata in figura 2 e.  Poi mettiamo la seconda metà della doppia mela (quella ridotta a ciliegia) tra le due estremità della pinza appena costruita e quindi riuniamo assieme queste due estremità. La superficie della pallina che abbiamo marcato con I’ sarà incollata sulla superficie I dalla quale è stata originariamente separata e le facce tagliate II e II’ devono essere fatte combaciare. Alla fine otteniamo una ciambella, bella e liscia.

Qual è il punto di tutto questo?

Proprio nessuno, a parte quello di proporvi un esercizio di geometria immaginativa, un tipo di ginnastica mentale che vi aiuterà a capire altre strane cose come lo spazio curvo e lo spazio chiuso in se stesso.

Se volete spingere un po’ oltre la vostra immaginazione, ecco qui un’”applicazione pratica” della procedura appena descritta.

Anche il nostro corpo ha la forma di una ciambella sebbene probabilmente non ci abbiate mai pensato. Infatti, nei primi stadi del suo sviluppo (stadio embrionale) ogni organismo vivente [animale] attraversa lo stadio conosciuto con il nome di “gastrula”, durante il quale possiede una forma sferica percorsa da un ampio canale. Attraverso una delle aperture di questo canale entra il cibo e attraverso l’altro esce quello che rimane del cibo dopo che il corpo ha preso tutto quello che può utilizzare di esso. Negli organismi completamente sviluppati il canale interno diventa molto più sottile e complicato, ma il principio rimane lo stesso e tutte le proprietà geometriche di una ciambella rimangono inalterate.

Ebbene, dato che siamo delle ciambelle, cerchiamo ora di immaginare una trasformazione inversa di quella mostrata nella figura 2: cerchiamo di trasformare il nostro corpo (mentalmente!) in una doppia mela con una galleria circolare al suo interno. In particolare scopriamo che, mentre le varie parti del nostro corpo si sovrappongono una con l’altra, formando il corpo della “doppia mela”, l’intero universo, inclusa la Terra, la Luna, il Sole e le stelle, saranno schiacciate dentro alla galleria circolare interna!

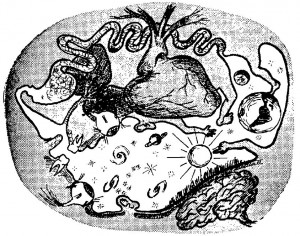
Cerchiamo di fare un disegno di come potrebbe sembrare e, se lo facciamo bene, lo stesso Salvador Dalì riconoscerà la nostra superiorità nell’arte surrealistica! (figura 3).

Non possiamo concludere questa sezione, così lunga, senza qualche discussione sui corpi destrorsi e sinistrorsi e sulla loro relazione con le proprietà generali dello spazio. Il problema potrebbe essere introdotto nel modo più conveniente facendo riferimento ad un paio di guanti. Se confrontiamo due guanti di uno stesso paio (figura 4),

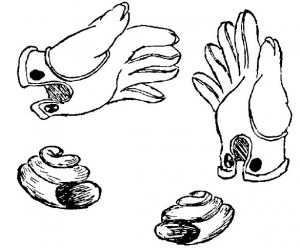
scopriremo che sono identici in tutte le loro misure e, nonostante ciò, rimane una grande differenza tra loro dato che non possiamo mettere la mano destra nel guanto sinistro e viceversa. Possiamo provare a girarli e piegarli come si vuole, ma il guanto sinistro rimarrà sinistro e il destro rimarrà destro. La stessa differenza tra oggetti destrorsi e sinistrorsi po’ essere notate nelle scarpe, nei meccanismi di sterzo delle automobili (tra il tipo americano e inglese), le mazze da golf e molti altri oggetti.

D’altra parte, oggetti come un cappello, una racchetta da tennis, e molte altre cose non mostrano tali differenze; nessuno sarebbe così scemo da ordinare in un negozio una dozzina di tazzine per mancini e sarebbe sicuramente uno scherzo se qualcuno vi chiedesse in prestito una pinza per mancini.

Qual è la differenza tra queste due categorie di oggetti? Pensandoci un po’ si noterà che gli oggetti come il cappello o le tazze da tè possiedono quello che chiamiamo un piano di simmetria lungo il quale ciascuno di essi può essere tagliato in due parti identiche. I guanti e le scarpe invece non possiedono alcun piano di simmetria e possiamo provare quanto vogliamo ma non riusciremo mai a tagliare un guanto in due parti identiche. Se un oggetto non possiede un piano di simmetria ed è, come si dice, “asimmetrico”, sarà obbligato ad essere presente in due possibili forme, la destrorsa e la sinistrorsa. Questa differenza non è presente solo negli oggetti costruiti dall’uomo come i guanti o mazze da golf, ma è anche molto frequente in natura. Per esempio, esistono due varietà di lumache, che sono identiche in tutte le loro caratteristiche, ma che differiscono solo nel modo in cui costruiscono la loro casa: una varietà con guscio destrorso [la cui spirale si sviluppa in senso orario partendo dal centro], mentre l’altra possiede un guscio sinistrorso. Addirittura le molecole, cioè le piccolissime particelle che costituiscono le varie sostanze, possiedono spesso forme destrorse e sinistrorse, come i guanti o i gusci di lumaca. Non possiamo vedere le molecole, ovviamente, ma la loro asimmetria si manifesta nelle forme dei cristalli e in alcune proprietà ottiche di queste sostanze. Ci sono, ad esempio, due diversi tipi di zucchero, i destrogiri e i levogiri e, ci crediate o no, esistono anche due tipi di batteri che si nutrono di zucchero, ciascuno dei quali consuma il tipo di zucchero corrispondente.

Come abbiamo detto, sembra del tutto impossibile trasformare un oggetto destrorso, ad esempio un guanto, in uno sinistrorso. Ma è proprio vero? Oppure si può immaginare un qualche tipo complicato di spazio in cui ciò sia possibile? Per rispondere a questa domanda, esaminiamola da punto di vista dei piatti abitanti di una superficie che può essere osservata dal nostro superiore sguardo tridimensionale. Osserviamo la figura 5 che rappresenta qualche esempio di possibili abitanti di “terrapiatta”, cioè di uno spazio a due sole dimensioni. L’uomo in piedi con i grappoli d’uva in mano potrebbe essere chiamato “uomo faccia” dato che ha una faccia ma non un profilo. L’animale invece è un “asino profilo” o, per essere più precisi, un “asino con profilo che guarda a destra”. Ovviamente si potrebbe disegnare anche un “asino con profilo che guarda a sinistra” e, dato che entrambi gli asini sono confinati alla superficie, dal punto di vista bidimensionale essi sono diversi nello stesso modo in cui, nel nostro spazio tridimensionale il guanto destro è diverso dal guanto sinistro. Non possiamo sovrapporre un “asino sinistro” con un “asino destro” perché, se tentiamo di mettere assieme i loro nasi e le loro code, saremmo costretti a rovesciare uno dei due asini e le sue zampe scalcerebbero l’aria invece di stare ferme appoggiate al suolo.

Ma se si toglie un asino dalla sua superficie, lo si gira nello spazio e lo si rimette sul piano, i due asini diventeranno identici. Per analogia si potrebbe dire che un guanto destro può essere trasformato in un guanto sinistro togliendolo dal nostro spazio, portandolo nella quarta dimensione e ruotandolo adeguatamente prima di riportalo giù. Ma il nostro spazio fisico non ha la quarta dimensione e il metodo appena descritto deve essere considerato del tutto impossibile. C’è qualche altro modo?

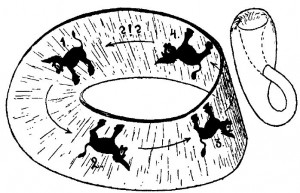
Ebbene, torniamo di nuovo al nostro mondo bidimensionale ma, invece di considerare una superficie piana come nella figura 5, investighiamo le proprietà della cosiddetta “superficie di Möbius”. Questa superficie, chiamata così dal nome del matematico tedesco che la studiò per primo nel diciannovesimo secolo, può essere costruita facilmente con un normale nastro di carta incollato ad anello. Una delle estremità deve essere ruotata di un giro prima di essere incollata all’altra estremità.

La figura 6 che ci mostra come è fatto il nastro. Questa superficie possiede molte proprietà peculiari. Una di queste proprietà può essere scoperta facilmente usando una forbice e ritagliando il nastro per tutta la sua lunghezza lungo una linea parallela ai bordi (cioè lungo le frecce disegnate nella figura). La cosa più normale che ci si aspetta è quella di ottenere due anelli separati. Fatelo e vedrete che la previsione era falsa: invece di due anelli otterrete un solo anello di lunghezza doppia rispetto all’originale e largo la metà.

Osserviamo adesso cosa accade ad un asino nero quando si mette in cammino lungo il nastro di Möbius. Supponiamo che esso inizi alla posizione 1 (vedi figura 6) come un “asino di profilo rivolto a sinistra”. L’asino procede passando attraverso le posizioni 2 e 3 che sono chiaramente visibili nel disegno e finalmente ritorna alla posizione iniziale. Ma per nostra e sua sorpresa, l’asino ora si trova in una posizione scomoda, con le zampe rivolte in alto. Se vuole, può benissimo girarsi e appoggiare di nuovo le zampe al pavimento ma in questo caso sarà rivolto nella direzione sbagliata.

In breve, camminando lungo la superficie di un nastro di Möbius, il nostro asino dal “profilo sinistro” è diventato un asino dal “profilo destro”. Non solo: rendiamoci conto che ciò è accaduto senza che l’asino sia uscito dalla sua superficie per girarsi nello spazio. Così abbiamo scoperto che in una superficie attorcigliata un oggetto destrorso può essere trasformato in sinistrorso e viceversa, semplicemente trascinandolo lungo la superficie ritorta. Il nastro di Möbius rappresentato nella figura 6 è solo una parte di una superficie generale conosciuta come “bottiglia di Klein” (rappresentata a destra), che possiede una sola faccia ed è chiusa in se stessa dato che non possiede bordi. Se questo è possibile in una superficie bidimensionale, la stessa cosa deve essere possibile nel nostro spazio tridimensionale se esso venisse adeguatamente attorcigliato. Naturalmente non è facile immaginare una torsione di Möbius dello spazio. Non possiamo vedere il nostro spazio dall’esterno come invece ci è stato possibile osservando la superficie dell’asino ed è sempre difficile vedere delle cose con chiarezza quando siamo dentro ad esse. Ma non è per niente impossibile che lo spazio astronomico sia chiuso in sé e magari attorcigliato come un nastro di Möbius.

Se ciò fosse realtà, i viaggiatori dello spazio potrebbero tornare mancini e con il cuore nella parte destra del loro torace e i fabbricanti di guanti e scarpe potrebbero semplificare notevolmente il loro lavoro facendo solo un tipo di scarpa e di guanto e far viaggiare la metà della produzione attorno all’universo per ritornare con la forma adatta all’altra metà dei piedi e delle mani del mondo.

Con questo pensiero fantasioso si conclude la nostra discussione sulle inusuali proprietà degli spazi inusuali.

Capitolo precedente: Geometria senza misure

Capitolo successivo: Il tempo è la quarta dimensione