Proprietà inconsuete dello spazio
- Miriadi di granelli di sabbia e di chicchi di frumento
- Storia della fine del mondo
- Una stampante “universale”
- Come contare l’infinito
- La matematica più pura
- La misteriosa radice di meno uno
- Proprietà inconsuete dello spazio
- Geometria senza misure
- Rovesciare lo spazio
- Il tempo è la quarta dimensione
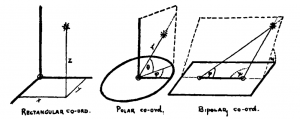
Noi tutti sappiamo cos’è lo spazio, ma ci troveremmo in una situazione piuttosto imbarazzante se ci venisse chiesto di definire esattamente cosa intendiamo con questa parola. Probabilmente diremmo che lo spazio è ciò che ci circonda e nel quale ci muoviamo, avanti e indietro, a destra e a sinistra, in alto e in basso. L’esistenza di tre direzioni perpendicolari, reciprocamente indipendenti, rappresenta una delle più importanti proprietà dello spazio fisico nel quale viviamo; diciamo che lo spazio è a tre direzioni o tridimensionale. Ogni posizione nello spazio può essere indicata riferendosi a queste tre direzioni. Se visitiamo una città che non conosciamo e chiediamo al receptionist dell’albergo dove si trova l’ufficio di una certa ditta famosa, egli potrebbe rispondere così: “Vada a sud per quattro isolati, poi prosegua per due isolati a destra e quindi salga al settimo piano”. I tre numeri forniti sono noti come coordinate e si riferiscono, in questo caso, alle relazioni tra le strade in una città, i piani di un edificio e il punto di origine rappresentato dalla hall dell’albergo. E’ chiaro comunque che le indicazioni per raggiungere quell’ufficio possono essere fornite partendo da un qualsiasi altro albergo della città, usando un sistema di coordinate che esprimerebbe correttamente la relazione tra il nuovo punto di partenza e la destinazione, e che le nuove coordinate possono essere espresse per mezzo di quelle vecchie con una semplice procedura matematica, a patto che si conosca la relazione tra il vecchio e il nuovo sistema di riferimento. Questo procedimento è noto come trasformazione di coordinate. Si può aggiungere qui che non è per nulla necessario esprimere le tre coordinate per mezzo di numeri indicanti distanze; infatti, in certi casi, è più conveniente usare coordinate angolari.
Così, ad esempio, mentre nella città di New York gli indirizzi sono facilmente identificabili per mezzo di un sistema di coordinate rettangolari rappresentate da strade e viali (streets e avenues), il sistema di indirizzi della città di Mosca ne guadagnerebbe sicuramente se fosse trasformato in coordinate polari. La vecchia città crebbe attorno alla fortezza del Cremlino per mezzo di strade divergenti a sviluppo radiale e diversi viali concentrici così che sarebbe naturale indicare una certa casa situandola, ad esempio, a venti isolati nord-nordest dalle mura del Cremlino.
Altri classici esempi di coordinate rettangolari e polari sono ad esempio due edifici di Washington D.C., il Navy Department e il Pentagono, noti a tutti per gli eventi della Seconda Guerra Mondiale.
Nella figura si forniscono tre esempi che mostrano come un punto nello spazio può essere identificato in diversi modi per mezzo di tre coordinate, alcune delle quali sono distanze, altre angoli. Ma, qualsiasi sistema si scelga, avremo bisogno sempre di tre dati visto che abbiamo a che fare con uno spazio tridimensionale.
Sebbene sia difficile per noi, con il nostro concetto tridimensionale dello spazio, immaginare superspazi nei quali ci siano più di tre dimensioni (anche se, come vedremo più avanti, questi spazi esistono), ci è facile concepire un sottospazio con meno di tre dimensioni. Un piano, la superficie di una sfera e, di fatto, qualsiasi altra superficie, sono esempi di sottospazi bidimensionali dato che la posizione di un punto sulla superficie può sempre essere descritta per mezzo di due soli numeri. In modo simile una linea (retta o curva) è un sottospazio unidimensionale ed è necessario un solo numero per descrivere una posizione. Possiamo anche affermare che il punto è un sottospazio a zero dimensioni perché in un punto non ci possono essere due diverse posizioni. Comunque, chi mai potrebbe essere interessato ai punti?
Essendo noi delle creature tridimensionali, ci risulta molto più facile capire le proprietà geometriche delle linee e delle superfici perché le possiamo osservare “dal di fuori”; le proprietà dello spazio tridimensionale, invece, sono più difficili da capire perché noi stessi ne facciamo parte.
Questo spiega anche come mai ci è facile immaginare una linea curva o una superficie curva mentre ci sbalordisce l’idea che anche lo spazio tridimensionale potrebbe essere curvo.
Comunque, con un po’ di pratica e con la comprensione di cosa si intende realmente per “curvatura”, troverete che il concetto di spazio tridimensionale curvo è molto semplice e, verso la fine del prossimo capitolo, discuteremo con facilità (lo spero!) di quello che a prima vista ci può sembrare una nozione orribile: la curvatura dello spazio quadridimensionale.
Capitolo precedente: La misteriosa radice di meno uno
Capitolo successivo: Geometria senza misure
Copyright © 2024 | MH Purity lite WordPress Theme by MH Themes