Geometria senza misure
- Miriadi di granelli di sabbia e di chicchi di frumento
- Storia della fine del mondo
- Una stampante “universale”
- Come contare l’infinito
- La matematica più pura
- La misteriosa radice di meno uno
- Proprietà inconsuete dello spazio
- Geometria senza misure
- Rovesciare lo spazio
- Il tempo è la quarta dimensione
Sebbene ciò che ricordiamo della geometria (1) imparata a scuola sia soprattutto una serie interminabile di teoremi che descrivono le relazioni numeriche tra le distanze e tra gli angoli (come ad esempio il teorema di Pitagora che definisce la relazione tra i lati di un triangolo rettangolo) la realtà è che gran parte delle proprietà fondamentali dello spazio non richiede nessun tipo di misure, né di lunghezze, né di angoli. Il settore della geometria che si occupa di questi argomenti è noto come analysis situs o topologia (2) ed è una delle branche della matematica più difficili e provocatorie.
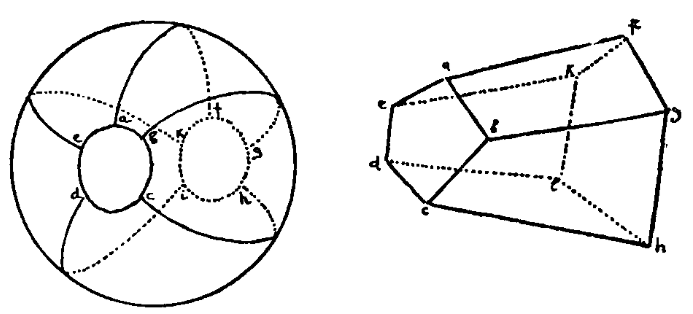
Per fare un semplice esempio di un tipico problema topologico consideriamo una superficie geometrica chiusa come quella di una sfera, suddivisa in varie regioni da una rete di linee. Possiamo predisporre una figura di questo tipo (fig.1) segnando alcuni punti sulla superficie e poi congiungendoli tra loro con delle linee che non si intersecano.
Qual è la relazione tra il numero di punti iniziali, il numero di linee in comune tra regioni adiacenti e il numero di regioni?
Innanzitutto risulta evidente che se al posto della sfera prendiamo uno sferoide, come ad esempio una zucca, o un oggetto allungato come un cetriolo, il numero di punti, di linee e di regioni è esattamente lo stesso che nel caso della sfera perfetta. In effetti, possiamo utilizzare una qualsiasi delle superfici chiuse che si possono ottenere da una palla di gomma, stirandola, schiacciandola, modificandola a piacere, a patto di non tagliarla o strapparla: rispettando queste regole, sia la formulazione della domanda che le risposte non cambieranno minimamente.
Questo fatto presenta un’impressionante contrasto con le comuni relazioni numeriche della geometria (come ad esempio le relazioni che ci sono tra le dimensioni lineari, le aree delle superfici e i volumi dei solidi geometrici). Senza dubbio, tali relazioni sarebbero materialmente distorte se si tirasse un cubo trasformandolo in un parallelepipedo o se si schiacciasse una sfera trasformandola in una frittella.
Una delle cose che possiamo fare con una sfera suddivisa in un certo numero di regioni è quella di appiattire le regioni in modo da trasformare la sfera in un poliedro; le linee che separano le regioni diventano gli spigoli del poliedro e i punti originali diventano i suoi vertici.
Perciò, possiamo riformulare il nostro problema, senza cambiarne il senso, e trasformarlo in una domanda concernente la relazione tra il numero di vertici, spigoli e facce di un poliedro di qualsiasi tipo.
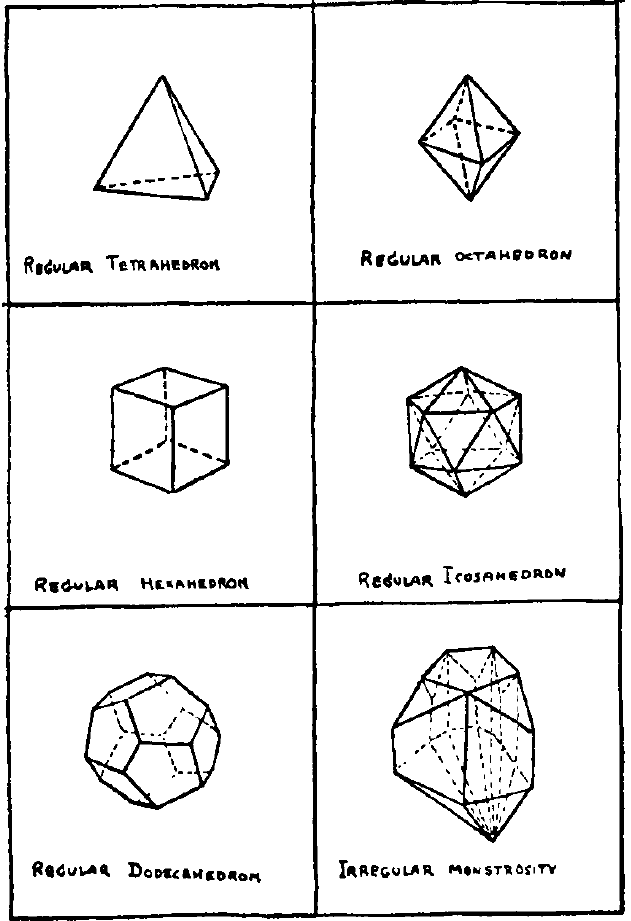
Figura 2 – Cinque poliedri regolari (gli unici possibili) e una “mostruosità irregolare”
Nella figura 2 vediamo cinque poliedri regolari, cioè quelli le cui facce hanno un ugual numero di lati e vertici, e un poliedro irregolare, disegnato a caso [irregular monstruosity].
Possiamo contare i vertici, i lati e le facce di ciascuno di questi poliedri. Qual è la relazione tra questi tre numeri, a patto che esista? Contiamoli e compiliamo una tabella come la seguente:
| Nome |
V numero di vertici |
E numero di lati |
F numero di facce | V+F | E+2 |
| Tetraedro (piramide) | 4 | 6 | 4 | 8 | 8 |
| Esaedro (cubo) | 8 | 12 | 6 | 14 | 14 |
| Ottaedro | 6 | 12 | 8 | 14 | 14 |
| Icosaedro | 12 | 30 | 20 | 32 | 32 |
| Dodecaedro o pentagono-dodecaedro | 20 | 30 | 12 | 32 | 32 |
| “Mostruosità” | 21 | 45 | 26 | 47 | 47 |
A prima vista i numeri delle colonne V, E e F non sembrano avere nessuna relazione, ma dopo attento studio si scopre che la somma dei numeri contenuti nelle colonne V e F supera il numero della colonna E di due unità. Così possiamo scrivere la seguente relazione matematica:
$$V + F = E + 2$$
Questa relazione vale solo per i poliedri indicati nella tabella o può essere estesa a tutti i poliedri? Se provate a disegnare altri tipi di poliedri scoprirete che la relazione vale sempre. Sembra che la relazione $V+F=E+2$ sia un teorema matematico generale di natura topologica, dato che la relazione non dipende dalle lunghezze dei lati o dalle aree delle facce ma riguarda solo il numero di unità geometriche coinvolte (vertici, spigoli, facce).
La relazione che abbiamo scoperto tra vertici, spigoli e facce dei poliedri fu notata per la prima volta dal matematico francese del diciassettesimo secolo René Descartes e fu dimostrata qualche tempo dopo da un altro genio matematico: Leonard Euler da cui il teorema prende il nome.
Segue qui la completa dimostrazione del teorema di Eulero secondo il testo del libro di R.Courant e H.Robbins, What is mathematics? tanto per far vedere come si trattano le questioni topologiche.

“Per dimostrare la formula di Eulero, immaginiamo che il poliedro sia vuoto e con le facce fatte di gomma sottile (fig. 3a). Se tagliamo una delle facce, possiamo deformare le altre facce fino ad appiattire il poliedro (fig. 3b). Ovviamente cambieranno sia le aree delle facce, sia gli angoli tra gli spigoli. La rete di spigoli e di vertici conserverà lo stesso numero di spigoli e vertici del poligono originale, mentre il numero di poligoni diminuirà di uno, visto che ne abbiamo tagliato uno. Possiamo vedere che per la rete piana vale la relazione:
$$V-E+F=1$$
Se si tiene conto anche della faccia tagliata, la relazione diventa quella del poliedro originale:
$$V-E+F=2$$
Ora “triangoliamo” la rete piana in questo modo: se un poligono non è un triangolo, ne tracciamo la diagonale. Ogni volta che tracciamo una diagonale il risultato è quello di incrementare di $1$ sia $E$ che $F$ e in questo modo si conserva il valore $V-E+F$. Continuiamo a triangolare tutte le facce finché la figura consiste solo di triangoli (figura 3c). La rete triangolata conserva ancora il valore $V-E+F$ che aveva prima della triangolazione.
Alcuni triangoli hanno i lati lungo il perimetro della rete. Ci possono essere due tipi di triangoli “di confine” quelli come $ABC$ che hanno un solo lato lungo il perimetro e quelli con due. Prendiamo ogni triangolo di confine e togliamo il lato che non è in comune con un altro (figura 3d). Ad esempio, dal triangolo $ABC$ togliamo il lato $AC$ e la faccia, lasciando soli i vertici $A$, $B$ e $C$ e i due lati $AB$ e $BC$, mentre dal triangolo $DEF$ togliamo i lati $DF$ e $FE$ e il vertice $F$.
La rimozione di un triangolo del tipo $ABC$ decresce $E$ e $F$ di $1$, mentre $V$ non cambia, e in questo modo $V-E+F$ rimane sempre uguale. La rimozione di un triangolo del tipo $DEF$ decresce $V$ di $1$, $E$ di $2$ e $F$ di $1$ e così $V-E+F$ rimane ancora inalterato. Rimuovendo successivamente tutti i triangoli che hanno i lati sul perimetro si rimane alla fine con un solo triangolo con i suoi tre lati, tre vertici e una faccia. In questa rete, che è la più semplice possibile, vale ancora la stessa relazione:
$$V-E+F = 3 – 3 + 1 = 1$$
che è la relazione valida per un qualsiasi poliedro con una faccia in meno. Concludiamo che $V-E+F=2$ è la relazione valida per un poliedro completo qualsiasi. La formula di Eulero è dimostrata”.
Una delle conseguenze interessanti della formula di Eulero è la dimostrazione che ci possono essere solo cinque poliedri regolari, e cioè quelli mostrati dalla figura 2.
Leggendo con attenzione la discussione di queste ultime pagine potrete notare che c’è un’assunzione nascosta che limita considerevolmente la nostra scelta sia per il disegno dei poliedri, che nel ragionamento matematico che dimostra il teorema di Eulero. Ci siamo limitati solo ai poliedri che non hanno nessun foro che li attraversa, e quando parliamo di fori non intendiamo qualcosa come un foro su un pallone di gomma, piuttosto qualcosa come il foro di una ciambella o il foro di un pneumatico di gomma.
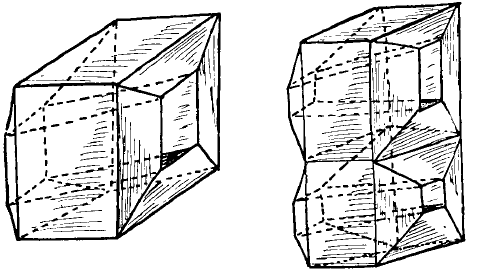
Un’occhiata a questa figura 4 chiarirà la situazione. Vediamo qui due diversi oggetti geometrici, che possono essere chiamati poliedri come abbiamo chiamato poliedri quelli della figura 2.
Vediamo se il teorema di Eulero si può applicare anche a questi nuovi poliedri.
Nel primo caso contiamo $16$ vertici, $32$ lati e $16$ facce; perciò $V+F=32$ mentre $E+2=34$. Nel secondo caso ci sono $28$ vertici, $46$ spigoli e $30$ facce, quindi $V+F=58$ e $E+2=48$. Ancora sbagliato!
Perché? Qual è il motivo per cui il teorema di Eulero fallisce in questi casi?
Il problema è dovuto al fatto che, mentre i poliedri che abbiamo considerato all’inizio si possono paragonare ad una palla di gomma, i poliedri con il foro sono simili piuttosto ad un pneumatico o ad una forma ancora più complicata. A questi poliedri il teorema non si può applicare perché non si può seguire lo stesso procedimento di dimostrazione. Ci era stato chiesto di “tagliare una delle facce del poliedro e di deformarne la superficie fino a distenderlo su un piano”.
Se provate a prendere un pallone di gomma e tagliare con la forbice una parte della sua superficie non farete fatica a realizzare questa richiesta. Ma non riuscirete a fare la stessa cosa con un pneumatico, qualunque sia lo sforzo che facciate. Se lo sguardo alla figura (***)16 non vi convince, prendete un pneumatico e provate!
Comunque non dovete pensare che i poliedri complessi non esista una relazione tra $V$, $E$ e $F$. Per i poliedri a forma di ciambella o, in termini scientifici, a forma di toro, abbiamo $V+F=E$, mentre per il “brezel” abbiamo $V+F=E-2$. In generale:
$$V+F = E+ 2 -2N$$
dove $N$ è il numero di fori.
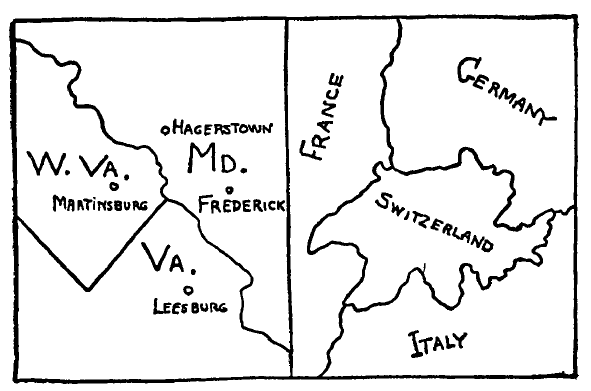
Un altro problema topologico strettamente connesso al teorema di Eulero è il cosiddetto “problema dei quattro colori”. Supponiamo di avere la superficie di una sfera suddivisa in un certo numero di regioni separate e che ci venga chiesto di colorare queste regioni in modo tale da non usare lo stesso colore per due regioni adiacenti (cioè con un confine comune). Qual è il minor numero di colori che dobbiamo usare per tale compito? E’ chiaro che, in genere, due soli colori non bastano, come nel caso di tre confini che si riuniscono in un solo punto, ad esempio quelli tra la Virginia, la Virginia Occidentale e il Maryland della mappa degli Stati Uniti (vedi figura 5). In questo caso abbiamo bisogno per forza di tre diversi colori.
Non è difficile trovare un esempio in cui sono necessari quattro colori, come nel caso della Svizzera durante l’annessione dell’Austria alla Germania [“Anschluss” del 1938](4).
Ma provate come volete: non riuscirete mai a costruire una mappa immaginaria, né su un globo né su un foglio di carta (5), in cui sono necessari più di quattro colori. Per quanto complicata sia la mappa, i quattro colori sono sempre sufficienti per evitare ogni confusione di confini.
Se questa affermazione è vera, si dovrebbe poterla provare matematicamente ma, nonostante gli sforzi di generazioni di matematici questa dimostrazione non è ancora stata fatta. Fino ad ora si è riusciti al massimo a dimostrare che sono sempre sufficienti cinque colori. Quest’ultima dimostrazione si basa sulla relazione di Eulero applicata al numero di stati, al numero dei loro confini e al numero dei punti tripli, quadrupli ecc. nei quali si incontrano più confini. Qui non tratteremo la dimostrazione perché è molto complicata e ci porterebbe lontano dal soggetto principale della discussione, ma il lettore può trovarla in vari testi di topologia e passare una piacevole serata (e forse una notte insonne) nella sua contemplazione. Il lettore potrebbe anche tentare di dimostrare che non cinque ma quattro colori sono sufficienti per dipingere qualsiasi mappa oppure, se è scettico sulla validità di questa affermazione, potrebbe riuscire a disegnare una mappa in cui quattro colori non sono sufficienti. Se dovesse avere successo nell’uno o nell’altro tentativo, il suo nome rimarrà negli annali della matematica pura per i secoli a venire.
[In realtà il teorema è stato dimostrato da Kenneth Appel e Wolfgang Hacken nel 1976 e quindi successivamente alla pubblicazione di questo libro; è interessante il fatto che la loro dimostrazione sia stata inizialmente contestata perché, essendo troppo complessa, richiede necessariamente l’aiuto di un computer].
Ironicamente, il problema dei colori, che elude con tale successo una soluzione per un globo o per una mappa piana, può essere risolto in modo relativamente semplice per superfici più complicate come quella della ciambella o del brezel. Per esempio, è stato dimostrato definitivamente che per colorare una qualsiasi mappa su una superficie a ciambella sono sufficienti sette colori e sono stati forniti esempi nei quali i sette colori sono in realtà necessari.
Allo scopo di avere un altro mal di testa, il lettore può prendere un pneumatico gonfiato e sette colori e provare a disegnare sulla sua superficie una mappa in cui ogni regione di un dato colore è adiacente ad altre sei regioni di colori diversi. Dopo averlo fatto potrà affermare di “conoscere la ciambella come le proprie tasche”.
note
(1) La parola geometria deriva da due radici greche, ge=”terra” o piuttosto “terreno”, e metrein=”misurare”. Sembra proprio che all’epoca dell’invenzione di questa parola i greci fossero interessati soprattutto alle loro proprietà.
(2) che significa, rispettivamente dal latino e dal greco, “studio del luogo”.
(4) Prima dell’annessione erano sufficienti tre colori: verde per la Svizzera, rosso per la Francia e l’Austria e giallo per la Germania e l’Italia.
(5) I casi della mappa piana e del globo sono uguali dal punti di vista del problema dei colori dato che, una volta risolto il problema sul globo, possiamo sempre praticare un piccolo foro in una delle regioni colorate e sviluppare la superficie sul piano. Ecco una tipica trasformazione topologica.
—-
Capitolo precedente: Proprietà inconsuete dello spazio
Capitolo successivo: Rovesciare lo spazio
Copyright © 2024 | MH Purity lite WordPress Theme by MH Themes